cc-5-1
还有一类并发控制的方法:多版本控制(multivesion concurrency control, MVCC)。每个写操作,都会产生一个新的版本,而不是覆写。这样做的好处是,一般不会reject一个操作(事务),即使按照history来说这个操作已经来迟了。而且也不会有太多额外的开销,因为对于下层的DM来说,为了支持recovery,也一般需要存储多个版本。只不过之前DM维护这些版本,对Scheduler不可见而已。
但是需要注意的是存储开销。之前的DM在一个事务提交之后,就会把before-image删掉;因此MVCC也需要一个类似的操作,需要不断地把旧的版本删除掉。但是因为有的旧版本会被某些活跃的事务用到,所以这里会产生一些同步的开销。
还有一点就是版本只是对Scheduler可见,而对用户不可见。用户依然是用 read[x]这样的表达方式,而不会指定具体的version。
正确性分析
之前用到的history的术语和定义,已经不太够了,因为这里多了一个版本的问题。需要两证history: multiversion(MV) history,表示DM的执行操作;single version(1V) history,表示从用户看来的执行操作。为了证明MVCC算法最后能达到SR,需要证明 MV history 最后等价于一个 SR的 1V history。
对于每个数据 x 来说,有多个版本 $x_i, x_j, …$,所以读写数据都要加上对应的下标。所以一般history会长成这个样子
$H_1=w_0[x_0]c_0w_1[x_1]c_1r_2[x_0]w_2[y_2]c_2$.
在构建等价1V history的时候,我们不能简单地把下标去掉,因为会丢失掉conflict信息。比如上面这个history,去掉之后变成:
$H_2=w_0[x]c_0w_1[x]c_1r_2[x]w_2[y]c_2$.
其实只有 $w_0[x_0], r_2[x_0]$ 会产生冲突。但是如果去掉下标之后,所有的x的操作都会冲突。而且结果也不等价,上面$T_1$最后读到的是 $x_0$,但是如果按照 $T_2$来,读到的是 $x_1$。所以需要定义一下等价:如果两个history有着相同的read-from关系,且最终的写是一样的,那么这两个history可以说是等价的。这个跟第二章定义的等价是一致的。
但是麻烦的是,即使 MV history是SR的,也未必能找到一个等价的 1V histroy。下面这个例子是一个 serial的MV history:
$H_3=w_0[x_0]w_0[y_0]c_0w_1[x_1]w_1[y_1]c_1r_2[x_0]r_2[y_1]c_2$
从MV history的角度来说,是serial的,但是从1V history的角度来说,对于 $T_2$,要么只读到 $T_1$的值,要么只读到 $T_2$的值。不应该读到中间值。所以找不出来一个。
由此可知,只有一部分的 serial(比serializable的条件更强) 的MV history 会等价于 serial 1V history, 称之为 1-serial MV history。如果是 1-serial MV history,那么任何一个read-from关系中,$r_i[x_j]$ 读到的是 $T_i$之前最新的一个 $T_j$写的x的值。
所有的 1-serial MV history 都会等价于一个 serial 1V history。所以如果想要证明一个MV history是SR的,需要证明它等价于一个 1-serial MV history。(PS:感觉这个应该是个充分条件,而不是必要条件)
MVCC 理论
上一章给的是一个感性的认识,这一章给出一些形式化的定义。这个跟之前的history理论有一些出入。首先有一组 事务 T= {$T_0, T_1, T_2, .., T_n$},每个事务自己有一个顺序(代码的顺序)$<_i$。有一个函数 $h$ 把对数据的访问,转为对具体版本的访问,比如 $w[x]$ 转为 $w[x_i]$。
所以一个complete multiversion history over T 可以视作一个偏序关系:
- 所有元素都来源于转化函数 h,把所有事务的操作转化之后的操作。
- 对于某一个事务里面的顺序,在 H 中依然得到保留
- 如果 $h(r_j[x]) = r_j[x_i]$ 那么, $w_i[x_i] < r_j[x_i]$。也就是说,只能读到已经写了的数据(废话)
- 事务内部自己会读到自己先前写的。即 if $w_i[x_i] < r_i[x_i]$,then $h(r_i[x]) = r_i[x_i]$
- $T_i$ read from $T_j$,那么$T_i$ commit的顺序也在后面(保留recoverable)
MV history的定义是某个 complete MV history的前缀。根据定义,C($H_{MV}$),即MV history中只取已经提交的,也是一个complete MV history,这一点可以根据定义来证明。
这里再重新定义下MV history的相等。首先,final write不用考虑,因为每个事务会写单独一个版本的值,彼此之间不会覆盖,所以只要读的内容是一样的即可。然后就是读:
$T_j$ read from $T_i$,当且仅当 $r_j[x_i] \in H$。
事实上,通过读请求(带数据的下标)我们就能得到read-from的关系了。比如上面通过$r_j[x_i]$ 就能的出来 $T_j$ read from $T_i$。然后就可以得出一个很漂亮的结论:
两个MV history相等当且仅当两个history中所有的操作是一样的。
下面定义一下 MV history 和 1V history的相等。首先在所有操作上,MV 和 1V的操作集,构成一个双射函数(即一一对应)。比如把 $r_i[x_i]$ 映射到 $r_i[x]$,而commit/abort 不变。而且因为写不会覆盖,所以不用关心写冲突。那么读冲突其实也只有一种,写后读,读后写是不可能的,因为如果一个version没产生,不可能读到它。所以我们只关心一种冲突: $w_i[x_i], r_j[x_i]$。如果read-from关系一样,则可以说这两个history一样。
在此基础上,我们可以构建MV history的序列图,SG(H),即每个事务是一个点,而有读写冲突关系的是一条边。很容易得知:
$H_1 \equiv H_2, 则 SG(H_1) = SG(H_2)$。
One-copy serializability
先定义serial MV history,和serial是一样的,每个事务依次执行,没有交互。One-copy serial的意思是,serial history,且对应任意read,读到的都是在这个事务之前的最新值。因此,之前的例子 $H_3$ 就不行。
如果一个MV history H, C(H)等价于一个 1-serial MV history,那么可以称之为 one-copy serializable (1SR)。下面给出证明 1SR 和一个 serial 1V history 等价。
对于一个MV history H, C(H) 等价于一个 serial 1V history,iff H 是 1SR。
充分性: 如果$H$是1SR,C($H$)等价于一个 1-serial MV history, $H_s$,可以构造这样的转化函数:$p_i[x_j]$ 转为 $p_i[x]$,即消掉读写数据的下标。这样得到一个1V history $H_s’$,操作顺序不变。因为$H_s$是 1-serial的,所以任何一个读,$r_j[x_i]$,读到的都是最新的值,即没有其他的写在 $T_i, T_j$之间,所以在$H_s’$中,$T_j$读到的也是$T_i$,即read-from关系不变。反过来,在$H_s’$中任何一个read-from关系,假设 $T_j$ read from $T_i$,且翻译$r_j[x]$的时候,翻译成了 $r_j[x_k], k \ne i$ (否则的话read-from 关系还是一样)。此时说明,存在 $w_k[x_k]$ 在 i,j之间。但是如果是这样的话,翻译过来,$T_j$应该read from $T_k$,跟得到的$H_s’$是矛盾的。因此,不可能存在这种情况,即$C(H) \equiv H_s’$.
必要性:首先C(H)等价于一个serial 1V ,$H_s’$。然后把$H_s’$转为$H_s$。规则是类似的,即$w_i[x]$会变成 $w_i[x_i]$, 读会变成读最新的版本。因为转化本身保留了read-from的性质,所以 $H_s’ \equiv H_s$。所以实际上 $C(H) \equiv H_s$,只要$H_s$是 serial 1V 即可。
首先需要证明$H_s$是一个complete MV history,即按照五个条件一个一个对比。非常简单,就不赘述了。接着$H_s$是 1-serial的。这个也很简单,因为是$H_s$转来得,按照定义,每个读只能读到最近的。所以 $H_s$是 1-serial的。命题得证。
1-serializability 理论
所以判定一个MVCC算法是否正确,就要判断所有它产生的历史记录是否是 1SR的。我们同样需要依赖序列图。之前,只关心具体某一个版本的数据冲突的图,作为 SG(H);现在需要加入考虑同一个数据不同版本之间的冲突,作为 MVSG(H)。
对于一个MV history,和一个数据 x,存在一个全序关系 $ \lessdot $ (书中的符号比较奇怪,画不出来)。MVSG(H, $\lessdot$)是在SG(H)的基础上添加若干条边做到的:任意三个不同的i,j,k ,$r_k[x_j], w_i[x_i]$,如果 $x_i \lessdot x_j $,需要把 $T_i -> T_j$加到 MVSG中;否则需要把 $T_k -> T_i$加进去。简单来说,就是如果一个读,读的不是另外一个写的值;要么这个写在读后面,要么这个写在读到的写的前面。即保证每次读都是之前最新的值。
举个例子,下面这个 MV history中,关系比较复杂。假设 $x_0 \lessdot x_2 , y_0 \lessdot y_1 \lessdot y_3, z_0 \lessdot z_3$。然后得到一个MVSG。其中,$T_1 -> T_2, T_1 -> T_3, T2 -> T_3$ 都是新加进去的。这些边都称之为 版本顺序边 (version order edge)
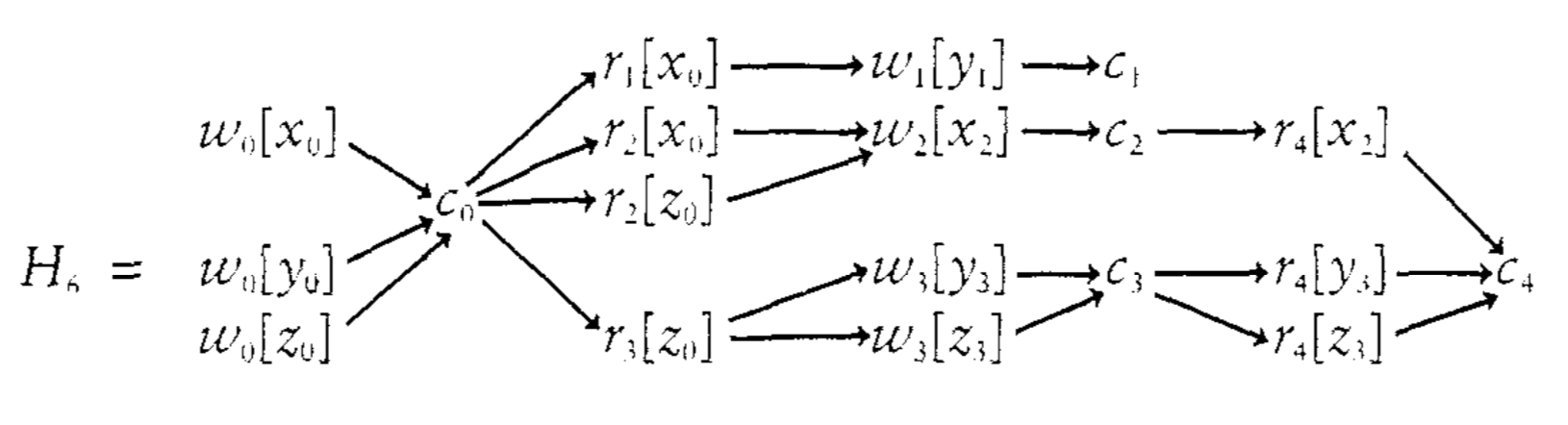

这些版本顺序边的好处,是把 MV -> 1V时候,丢掉的信息保存下来。
MV history 是 1SR, iff 存在一个版本序, MVSG(H, $\lessdot$) 是无环的.
证明跳过。
Multiversion Timestamp ordering
上面说了MVCC的理论基础,下面可以讨论具体实现方式。同样的,也可以用 2PL, TO, SGT 三种方式实现 MVCC。这一章先从 MVTO 开始,因为 TO最简单。
MVTO的思路比较简单,“假装”所有的操作都是按照 ts的顺序来的。在读的时候,选择一个最近的版本读;在写的时候,如果发现有读,ts在自己之后,却已经读了之前的数据,那么reject掉这个事务。为了保证recoverability,一个事务需要等它读的事务全都提交之后才能提交。
为了维护这样的性质,需要一个新的数据结构。每个x的每个版本,都有一个 interval($x_i$) = [wts, rts],wts是它自己的版本号;rts是目前最大的读。读的时候找到离自己最近的interval,然后更新rts(如果有需要的话)。写的时候,测试下自己的ts是否在某个interval之间,如果在就有问题,需要把自己干掉;否则的话新建一个interval。
正确性证明
证明也比较简单,首先 版本序很好定,就跟ts一样。然后证明 MVSG(H, $lesspot$)中无环即可。然后证明MVSG中,任意一条边的两个点,都可以得到 ts($T_1$) < ts($T_2$)。因为MVSG的边来源有两个,一个是SG中的边,一个是 read-from关系造成的边。分情况讨论下即可。
Multiversion 2PL
首先介绍的是一种基于两个版本的2PL。当写的时候,阻止别人读新写的值,同时也阻止其他的写;但是允许读旧的值。DM里面一个数据会有新旧两个版本。这个恰好和DM里面做recovery的逻辑相匹配,本来DM执行写的时候也会存一个before-image的版本。
在MV2PL中,多了一种锁,certify锁。他们之间的关系如下图所示。当一个事务正常执行的时候,正常拿读写锁;但是当要提交的时候,把所有写锁都升级成certify锁。之前所说,读写锁是可以并存的,所以certify锁的意义就是,在commit的时候,没有活跃的读。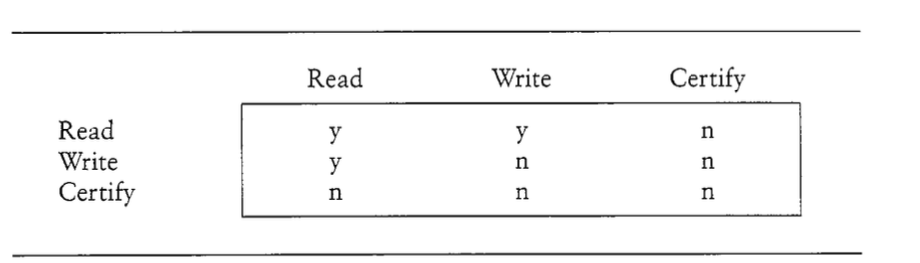
因为每次读的内容,都是已经commit的内容,所以这种机制天生的是 avoid cascading abort,也就是说是recoverable的。
正确性证明
先看几个 MV2PL的性质 其中 $f_i$表示第i个事务的certification:
- 对于每个transaction ,$f_i$在所有读写之前,在commit之后。(显然)
- 对于每个读 $r_k[x_j]$, 如果i不等于k,那么$c_j < r_k$;如果i=k,那么 $w_k[x_k] < r_k[x_k]$(也是显然)
- 如果 $w_k[x_k] < r_k[x_j]$,那么 k = j。也就是说如果一个事物内部,读肯定看到的是自己的写。
- $r_k[x_j], w_i[x_i]$ 同时存在,那么 $f_i 和 r_k$两个一定有一个严格的顺序。这个也是显然,因为两者会抢同一把锁。
- 如果 $w_i[x_i], 且 f_i < r_k[x_j]$, 那么 $f_i < f_j$。这个也是显然,否则k不会读不到它。
- 跟5对应,如果反过来,$r_k < f_i$,那么 $f_k < f_i$。因为$T_k$只有certification之后才会释放锁。
- 任意两个写操作冲突,那么他们的certification也是严格有序的。
2V2PL 产生的History都是1SR的。
proof: 通过1,2,3,首先能保证这是一个MV history。然后把版本序定义为按照certification的序(因为有7,所以一定有一个全序)。下面证无环即可。
首先看SG(H)中的边,假设 $T_i \rightarrow T_j$. 那么$T_j$有个读操作。因为性质2 $f_i < r_j[x_i]$。所以 $f_i < f_j$。
再看因为version edeg 带入的边。 $w_i[x_i], w_j[x_j], r_k[x_j]$。第一种情况 $w_i \lessdot w_j$,所以加的边是 $T_i \rightarrow T_j$,根据7,$f_i < f_j$。如果第二种情况 $w_j \lessdot w_i$,那么添加的边是 $T_k \rightarrow T_i$。根据条件4,$f_i < r_k[x_j]$或者 $r_k[x_j] < f_i$。如果是前者,根据5,则 $f_i < f_j$,这个跟 $w_j \lessdot w_i$矛盾。所以只能是否者,即 $r_k[x_j] < f_i$,根据6,$f_k < f_i$。
综上所述,MVSG中每一条边,$T_i \rightarrow T_j$,都能得到 $f_i < f_j$。所以MVSG是一个无环图,否则会出现f自己小于自己。
MVCC 混合方法
这里其实是为了解决read-only的事务。这里接受的方法是,对于RO的,用MVTO,对于updater,用strict 2PL。跟之前一样,updater的事务,会在commit的时候获得一个timestamp,然后再”真正“写数据库。但是跟之前不一样的是,每个写都会产生一个新的version。读的时候,会分配一个ts,这个ts比正在活跃(正在提交的)的事务的ts都要小,所以它能看到的都是一件提交了的,就保证了recoverability。
证明也简单,就证明所有的边的顺序都跟ts的顺序一样即可。