CC(2) "2. Serializability Theory(上)"

本文是《Concurrency Control》的第二章，介绍有关连续性的理论。通过这些理论，我们能够搞明白一个问题，什么情况下concurrency的执行是正确的。很多新的transaction算法都是需要证明该算法是serializable的。

Serializability Theory

2.1 History

Transaction

第一章中定义的transaction，是一系列读写操作的集合。从serializablity的角度，我们可以这么理解transaction：定义了一系列读写操作的先后顺序。每个读写的操作，对象是变量名，而不是实际的值。例如：

Procedure P begin
	start;
	temp:=Read(x);
	temp:=temp+1;
	Write(x,temp);
	Commit
end

可以用r_i[x] -> w_i[x] -> c_i来表示。后文中，我们会用r_ix来表示T_i对变量x的读写操作。c_i a_i表示commit或者abort。

比如一个transaction需要读x，y然后相加，将结果写到z里面。这就需要先读x,y，再写z，也就是说w₂[z]必须先于r₂[x]和r₂[y]，而两个读操作没有先后顺序的要求。

如果两个操作（即使不是同一个transaction的），读写同一个数据，也天然有一种先后顺序。读的结果取决于读操作和写操作的先后关系。

这里我们统一一种数学定义。所以操作的顺序可以表示为有序对（$ \sum, < $），其中，$ \sum $ 表示全部有序操作，< 表示顺序关系。所以，我们可以把 $ T_i $ 表示为($\sum_{i}, <_i$)。表示所有操作和顺序关系。

基于以上的基础，我们可以给出transaction一个更加精确的定义。一个transaction $T_i$ 是一组有着关系$<_i$的操作：

$ T_i \subseteq { r_i[x], w_i[x] } \bigcup { a_i, c_i } $
$ a_i \in T_i$ iff $c_i \notin T_i$
if t is $a_i$ or $c_i$, any other $p \in T_i, p <_i t $
if $r_i[x], w_i[x] \in T_i$, then either $r_i[x] <_i w_i[x]$ or $w_i[x] <_i r_i[x] $

翻译成人话就是：

操作类型就是读写，提交或者取消
提交和取消只能有一个。
提交和取消操作只能在其他操作之后
一个数据的读写必须有先后关系。

注意的是，我们这里只讨论了读写操作，一些其他的，比如赋值、条件语句，都没有被包括进来。为了证明一种调度算法的正确性，我们必须涵盖所有的情况。

不假设data item的初始值。
假设一个transaction钟，所有的写操作，都依赖于先于它的读操作。这明显是提高了限制条件。

History

对于多个transaction交替执行，它们的操作会互相交错。其中一种可能的顺序，我们称之为一个history。因为有可能有同时执行的操作，所以允许这两个操作没有先后关系。但是，一旦history指明了两个操作的关系，那么实际执行中有着确定的先后关系。

假设一个transaction的集合，T = {$T_1, T_2, …, T_n$}一个完整的History包括操作（T）和顺序关系($<_H$)两个部分。满足下面的条件（公式输入太麻烦，这里直接翻译）：

所有transaction中的操作。
所有transaction中的顺序关系是它的一个子集。也就是说，必须满足已有的顺序关系，同时还有可能新的关系（跨transaction的关系）
任意两个冲突操作（对一个data item，至少一个操作是写），必须有先后关系。

这应该很好理解，这里就不做解释了。有一种history是全排序，就是说所有的操作都有一个顺序。我们按顺序写下来比如下面的格式：
$r_1[x]r_3[x]w_1[x]c_1w_3[x]c_3$

2.2 Serializable History

上文定义了history，这里我们再定义何为serializable的history。

history的等价性

两个history，H H’,如果说结果一样，我们可以认为是等价的。具体来说：

有着相同的transaction，有着相同的操作。
有冲突的操作的执行顺序是一样的。$p_i, q_j$分别是$T_i, T_j$的两个操作，如果说$p_i <_H q_j $, 那么一定有 $p_i <_{H’} q_j$

因为两个没有冲突的操作，无论执行顺序是怎么样的，结果一定相同。所以执行结果完全取决于冲突操作的顺序。如下图所示，$H_2=H_3$，但是$H_4$不等。(图中有误，$T_3$中有一个应该是$w_1[y]$)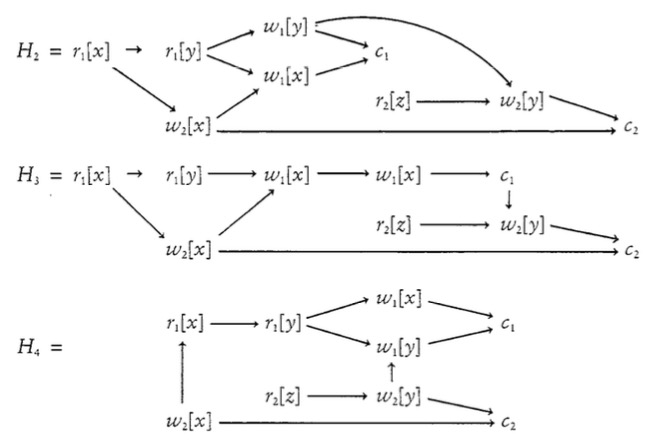

Serializable history

注意，一个serial的history是：任意两个transaction，其中一个的全部操作都在另外一个transaction之前。也就是说，每一个transaction都是一个原子操作，没有交叉。

而一个serializable的history指的是和任意一个serial history$H_s$等价的history。注意，这里的history必须是完整的。因为首先serial一定是完整的；其次如果有没有完成的操作，这实际上和数据库系统的一致性要求相违背。

所以可以换一种定义方式，一个history的commited projection（可以理解为只有commited的transaction算进去了，其它的不管）C(H)，等同于某个serial history。

2.3 The Serializability Theroem

这里到了本章的关键。对于一个H，我们可以画出一个serialization graph，记为SG(H)。该图中每一个节点表示一个transaction，箭头表示两个transaction之间有先后关系。即两个transaction中各有一个操作在同一个data上产生了冲突。箭头指向的方向表示后执行的一个。注意，有可能有环。下图就是一个SG的例子。因为$r_2[x]$先于$w_1[x]$和$r_3[x]$，故有一个$T_2$指向$T_1$和$T_3$的箭头。依次类推。其中$T_2$到$T_3$的箭头可以省去。

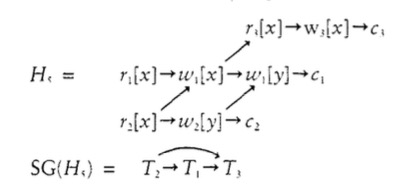
如果说$T_i \rightarrow T_j$ 表明i中有一个操作与j冲突，且i 先于j。所以如果该history有一个等价的serial history, $H_s$，$H_s$中必然会有i 先于 j.

反过来，如果SG是一个无环图，那我们一定能找到一个等价的serial history

定理2.1 一个history是serializable，当且仅当SG(H)是无环的。

proof: (if)如果SG(H)是无环的，我们假设$T_1,T_2,…,T_n$是SG(H)的节点。假设$i_1,i_2,,,,i_n$是1,2,3,…n的一个排列，其中$T_{i_1},T_{i_2},…,T_{i_n}$是SG(H)的拓扑排序。然后假设$H_s=T_{i_1},T_{i_2},…,T_{i_n}$。我们来证明两个history相同。

假设$p_i \in T_i, q_j \in T_j$,$T_i, T_j$都是已经commit的transaction。二者冲突，不妨设$p_i <_H q_j$。所以根据定义，在SG(H)中会有一条i指向j的箭头。因为拓扑排序的原因，所以$T_i$排在$T_j$前面。所以在$H_s$中，必然会有$p_i <_{H_s} q_j$，也就是说，$H_s$和H中所有冲突的操作的先后顺序都是一样的。

(onlyif) 如果H是SR，假设$H_s$是C(H)的等价serial history。$p_i \in T_i, q_j \in T_j$,两个操作冲突，不妨设$p_i <_H q_j$。因为C(H)=$H_s$，所以也有$p_i <_{H_s} q_j$。在SG(H)中有一个箭头从i到j，而在$H_s$中，i在j前面。

若有一个环，$T_1 \rightarrow T_2 \rightarrow … \rightarrow T_k \rightarrow T_1 $ 反应到$H_s$中，就是1在2前，2在3前,…，k在1前面，显然是不可能的。所以SG(H)中不可能有环。是一个无环图。

证毕

在证明过程中我们发现,SG(H)的拓扑排序可能不止一种，所以等价的serial history也可能不止一种。