CC(2) "2. Serializability Theory(下)"
第二章下半部分
2.4 Recoverable History
之前我们提过,一个正确的调度,不仅仅应该支持SR(serializable),同时也应该是Recoverable的。这一点还有很多具体的要求。比如防止连锁aborts和loss before image(A写,B写,A abort,同时改掉了B写的数据),也就是要“strict execution”。这些概念也可以用上面的语言来描述。
首先定义$T_i$读$T_j$的数据,这一说法的具体含义:
- $w_j[x] < r_i[x]$
- $a_j 不小于 r_i[x]$ and
- if there is some $w_k[x], w_j[x] < w_k[x] < r_i[x]$, then $ a_k < r_i[k]$
也就是说,j写了一个数据,在i读之前没有没有人写,即使有也在i读之前abort了。而且i自己abort必须在读之后。
同时,一个transaction也可以自己读自己的。
所以回顾RC(recoverable)的定义,任何时候$T_i$读$T_j$,并且$c_i \in H$,$c_j < c_i$,这样的history称为RC。
如果把条件改为$c_j < r_i[x]$,那么就是avoids cascading aborts(ACA)的history了。
strict的定义是,只要$w_j < o_i[x]$,那么,要么 $a_j < o_[x]$ or $ c_j < o_i[x] $。其中o表示r/w。也就是说,A写了数据,B想操作它,必须等他commit或者abort之后才可以。
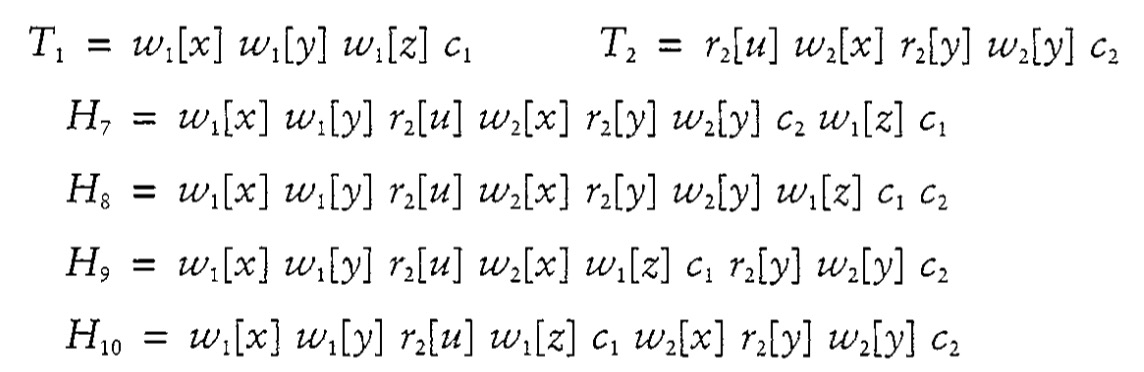
举个例子吧,上图中,$H_7$就是非RC的,因为2读了1,但是2先commit了。$H_8$是RC,但是非ACA,因为2读了1,但是没有等到1commit之后再读。而$H_9$是ACA,但是非ST(strict),因为2在1commit之前就写了。记住RC, ACA, ST, SR这几个标记,我们之后讨论都会用这几个省略符号(一个个敲英文单词太蛋疼)
定理2.2: $ ST \subset ACA \subset RC $
实际上大家应该能够猜出来。下面进行比较严格的证明。(所以这帮人把计算机上升成一门科学不是没有道理的)
Proof: 如果 $H \in ST$, $H$中$T_i读T_j$,数据是x。根据transaction read from的定义,所以$w_j[x] < r_i[x]且a_j不小于r_i[x]$,因为SR的定义,一定有$c_j < r_i[x]$。这就和ACA的定义是一样的了。换句话说,ST要求写数据之后,别人的读写必须在自己commit或者abort之后;而read from要求必须在读之前不能abort,所以为了满足条件,只能在读之前commit了。
现在$H \in ACA$,假设$T_i读T_j$,且$c_i \in H$.(不commit就没有讨论的必要了)。因为ACA的定义, $w_j[x] < c_j < r_i[x]$,又因为$r_i[x] < c_i$。所以$c_j < c_i$,所以$H$也是RC的。
但是SR和RC,ACA,ST是交叉而不是包含被包含的关系。具体见下图。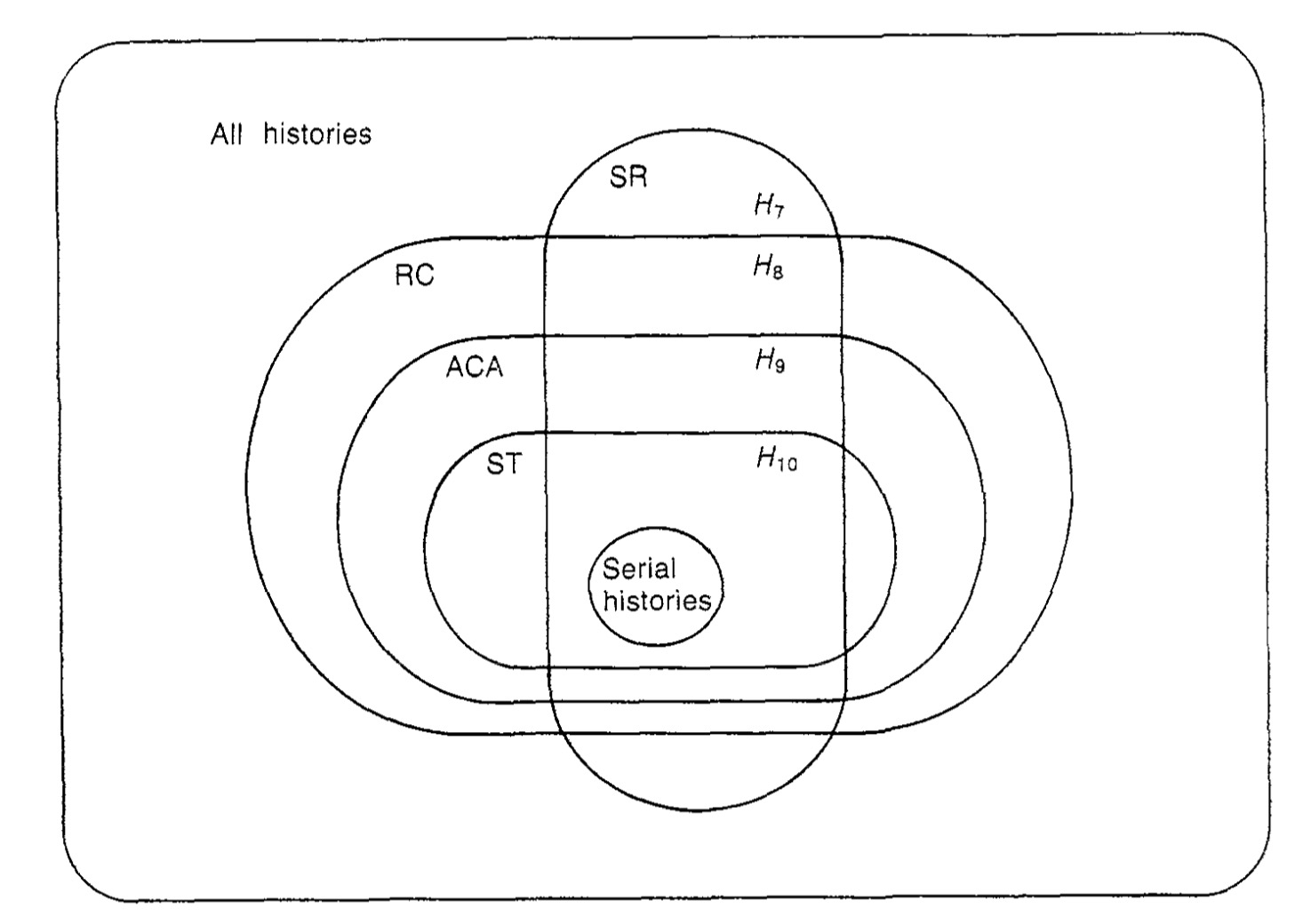
下面介绍一个很重要的概念,叫做prefixed commit-closed property。一个属性,如果对于H是真,那么对于任何H的前缀H’,该属性也满足C(H’)。这个概念的意义在于,DBS随时都有可能挂掉,恢复的时候只能恢复成C(H’)。比如说有一种属性是“正确”,所以C(H’)也必须是”正确“的。那么任何时候挂掉重启,都是“正确“的。(有点晦涩,意会一下)
之前讨论的RC,ACA,ST都是prefixed commit-closed property。下面证明serializability也是:
定理2.3: Serializability 是一个prefixed commit-closed property
Proof: H是SR,所以SG(H)是无环的。H’是一个前缀,所以SG(C(H’))是SG(H)的子图,所以也是无环的,所以H’是SR。证毕
2.5 读写之外的操作
我们之前的讨论,都是假设整个DBS只有读写两种操作,这显然是不可能的。
但是我们发现,之前讨论的核心概念是”冲突“,之前的概念是至少有一个是写操作;我们可以把这个概念扩充一下:两个操作的执行顺序会影响最终的结果(结果的意思是最终该操作返回的结果和它读到的数据)。进一步分析定理2.1,我们只用到了冲突这个概念,所以定理2.1还是成立的。
举个例子,有两个基本操作,increment和decrement,都是在原数据的基础上,进行加减。所以它们彼此之间是没有冲突的。再加上read,write,这四个操作我们可以画出一个兼容表。读只和读兼容,写和任何操作都不兼容;increment/decrement彼此兼容。
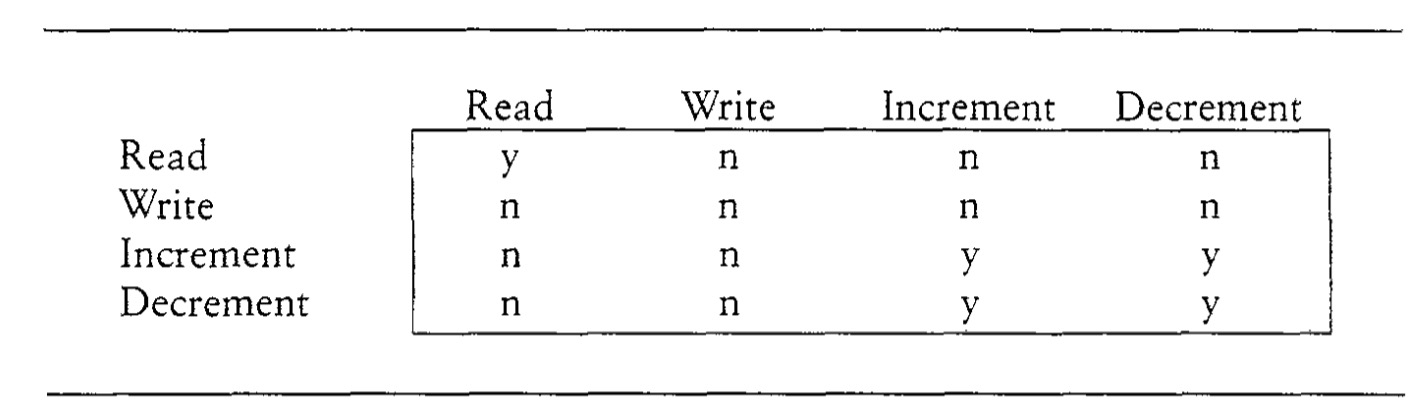
在此基础上,我们再画SG图,可以判断一个history是不是serializable的了。
2.6 View Equivalence
我们之前讨论了半天 history equivalence, 核心为了判断两个history是不是拥有相同的结果。结果呈现的状态就是所有没有被abort的transaction的写操作。
我们不知道每个transaction会写什么,我们只知道,它读了一些数据,然后根据读的数据写了一些数据。(依赖读操作的个数为0~n个)。所以,如果两个history读的数据来源是一样的,写的数据肯定会一样。所以可以得到两个结论:
- 如果两个history读的数据,是来自相同的写操作;那么两个history所有写操作,写的内容是一样的。
- 如果每一个数据x,最后一个写操作写入的数据一样,那么两个history是等价的。
关于第一点,这里做一个简单的解释。实际上用归纳法可以证明;
- 最开始初始化的数据都是相同的
- 如果某一个$w_i[x]$,其读取的数据来源在H和H’中也是相同的,其输出结果一定是相同的。
然后根据1,2可以递推,两个history所有写操作的结果一定是一样的。
我们定义final write为:$w_i[x] \in H, a_i \notin H$, any $w_j[x] \in H, (j \not \equiv i)$, either $w_j[x] < w_i[x]$ or $a_j \in H$, 然后定义history equivalence:
- 有着相同的transaction和操作;
- 任何$T_i, T_j$,其中$a_i, a_j \notin H, H’$,任意x,如果H中$T_i$从$T_j$读取x,那么H’中亦然
- 任何x,H中如果final write是$w_i[x]$,H’中亦然。
细细品味,这里的定义和之前history equivalence的定义(所有conflict操作的顺序是一样的)还是有所区别的。所以我们把这种称之为view equivalence,而之前的称为conflict equivalence
View Serializability
我们可以从上面的定义,引申出view serializability的概念:即H的任意前缀H’,C(H’)和某一个serial history 是view equivalent的。
为什么要强调任意前缀,我们举一个例子:
$H_12 = w_1[x]w_2[x]w_2[y]c_2w_1[y]c_1w_3[x]w_3[y]c_3$
如果根据view equivalence的定义,该history是等价于$T_1T_2T_3$的。首先没有transaction有读,所以第一条肯定满足;其次最后写的xy都是3,第二条也满足。
但是如果截取前缀,只看到$c_1$那一段,那么这一个history不等价于任何serial history。因为最后写x、y的分别来自1、2。
这样就破坏了commit-closed的特性。
可以证明,conflict serializable是view serializable的真子集。
定理2.4: 如果H是conflict serializable,那么一定是view serializable;反之不一定。
Proof: H是conflict serializable的,任意前缀H’,C(H’)一定conflict equivalence某个serial history$H_s$。
假设在c(H’)中$T_i$从$T_j$中读了数据x,那么$w_ij[x] <_{c(H’)} r_i[x]$且没有其他的写在二者之间。因为conflict serializable的定义,而且读写就是冲突操作,所以在$H_s$中,也保持这样的关系。$w_ij[x] <_{c(H’)} r_i[x]$且没有其他的写在二者之间。也就是说,在$H_s$中$T_i$从$T_j$中读了数据x。这样满足了条件1.
再看,如果c(H’)中最后一个写操作是$T_i$,那么没有一个k,使得$w_i[x] < w_k[x]$。所以,也不会在$H_s$中出现这样的现象,否则冲突关系就不一样了。所以也就满足了条件2
证明反之不成立举一个反例就可以了。比如上一个例子,$H_12$是view serializable的,但是画SG图我们可以发现,是有环的。所以反之不成立。
总结
第二章介绍完了,重要的概念就是history。对于serializable的要求,我们用history equivalence来证明一个history的可连续性,一个重要的方法就是画出SG;对于Recoverable的要求,我们给了read from的定义,然后用数学方法证明了几种调度策略的包含关系。
另外一点需要强调的是view equivalence和conflict equivalence的区别。前者是我们实际需要看到的,感官上的结果;后者更加严格一点。
下面几章会具体介绍调度算法,会用到这一章的理论来证明算法的正确性。