Distributed snapshot

1 背景

这篇文章是介绍Chandy和Lamport关于做分布式系统中snapshot的算法。原论文题为：《Distributed Snapshots: Determining Global States of Distributed Systems》

提到snapshot，我们想到的是为了容错，把状态记录到磁盘里面；然而这里的snapshot要有所区别，指的是整个系统的一个状态；相当于我们开了上帝视角，对着整个系统瞄了一眼，得到一个整体的状态。程序需要用这种状态去做一些判断或者计算。比如检测死锁，需要先有一个全局的信息，拿到这个快照之后再进行检测。

而一般意义上的状态,包括两个部分，节点状态和网络状态。节点状态很好理解，就是每个进程运行到什么程度；网络状态就是在快照的一瞬间，有哪些message在网络上飞。

然而困难之处在于，没有个global clock同步。比如一个naive方法，一个node发送snapshot的请求，所有节点停下来，然后返回一个ack，之后再统一进行snapshot。这样做的问题是，没有办法界定正在网络上飞的信息。如A机器发了n个信息，然后收到请求，停下来；同时B机器收到请求停下来，但是此时系统无法记录这n个信息。

因此，我们可以得出结论：没有一个观察者，可以一次性观察所有的node，得到一个snapshot，必须有多个观察者，得到多个snapshot，然后拼成一个；第二因为同步问题，并不能得到一个精确时间点上的snapshot。

然而这种拼凑的snapshot是有意义的。我们定义一种stable property，指的是某一个函数y,对于状态S，y(S)成立的话，对于所有的S’也成立，其中S’是由S转化得到的。典型的stable property有“运算结束了”（不可能结束之后又开始对吧），“系统死锁了”（死锁了不会自己开的）。所以在后文中，我们只要找到一个S’是当前全局状态S，通过某种执行可以达到的结果，那么也是有意义的。

2 系统模型

前面啰嗦了一大堆，就是为了普及一下背景知识。下面用一种比较严肃的语言，对系统模型进行精确的表述。

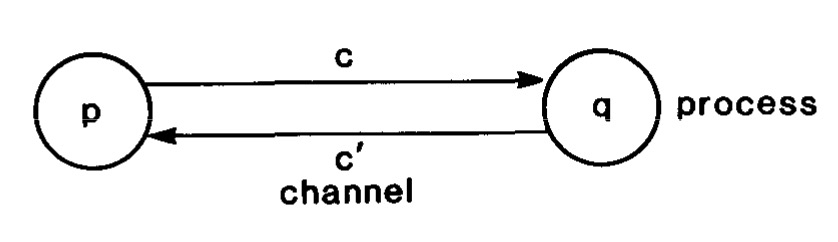
一个分布式系统由有限个process和有限个channel构成；channel是一个有向图，指的是两个进程之间的信息传递的通道。我们给出一下几种假设：

process上做 snapshot local state 是原子的
任意$n_1, n_2$,都会有一个道路(channel的集合)，从1到2.
process正常工作；
channel正常工作；
channel上的信息发送是FIFO

而process是由一系列状态和event定义的。状态很好理解，我们看一下event的状态。Event < p,s,s’,M,c>，其中：
p: process，s: 发射之前的状态，s’: 发射之后的状态，M: Message，c: channel

而整个系统的状态：S = $Us_n+Us_c$，也就是说所有的node的状态和所有channel状态的合集。

我们可以这么看整个系统，就是在event的驱动下，从一个状态转移到另外一个状态。可以据此画出状态转换图，可以是确定性的，也可以是不确定性的。这和单机的状态转换图并没有本质的区别。

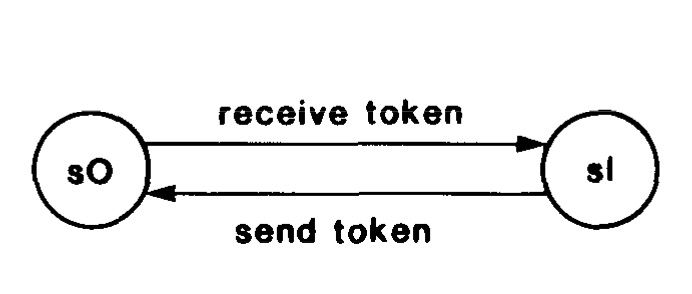
原文举了两个例子（本来不想赘述，但是和下文算法的获得有关），这里解释一个token的例子。下面两张图，分别描述了系统的结构和转化方式。首先两个process和两个channel，很好理解；然后每个process有两种状态，S0的时候需要接受一个token，然后变成S1；S1可以放弃token，然后变回S0。只有这两个变化方式。如果初始系统两个process，一个处于S0，一个处于S1，channel为空，那么可以得到一个确定性的状态转化图。

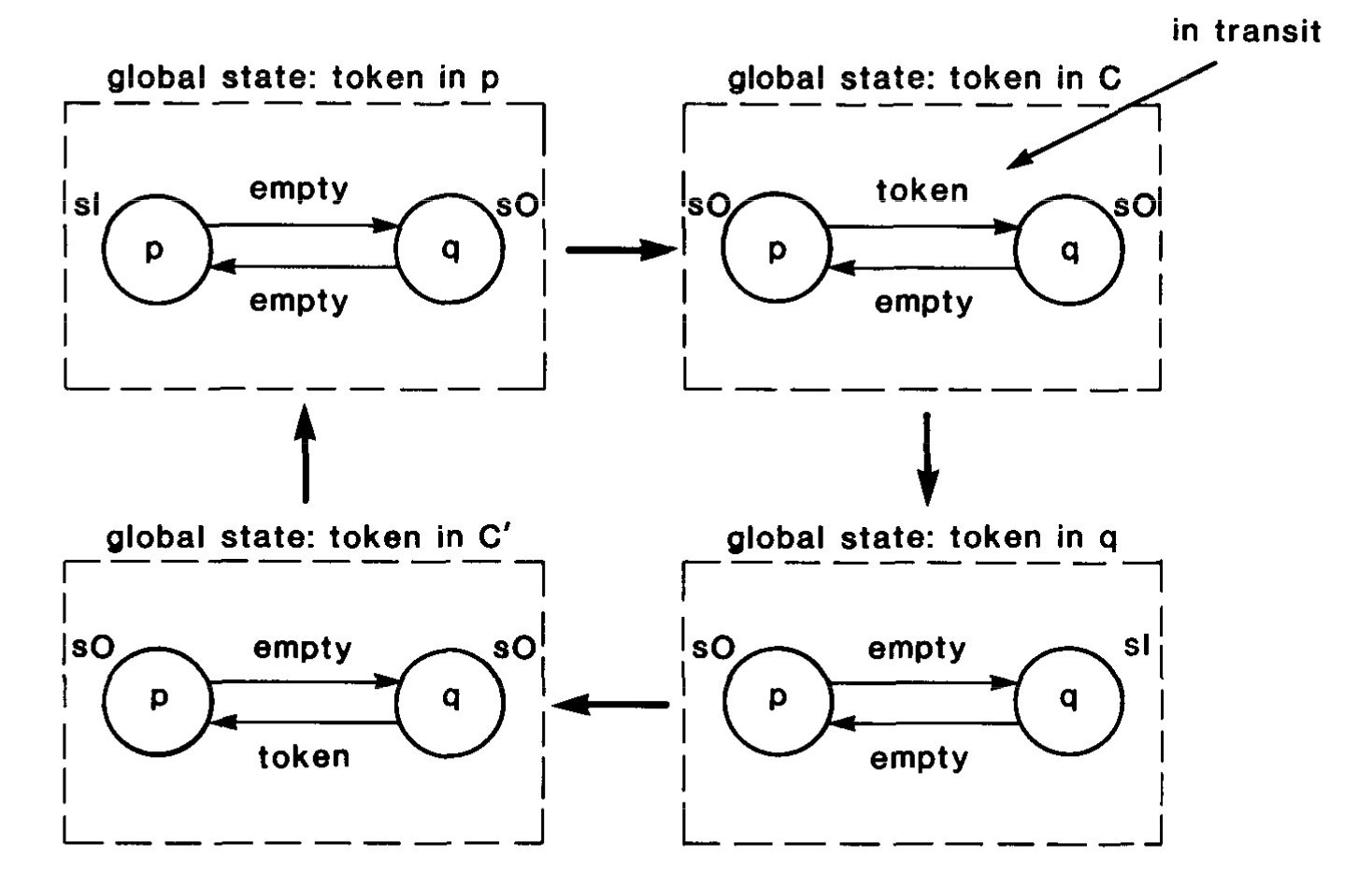
也就是说，开始的时候token在p上，p为S1；然后token被p释放，传到了channel c上，p变为S0；然后token传到了q上，q变为S1；最后q再把token还给p。

3 算法

3.1 想法的来源（很拗口，可以直接略过）

我们回到上面那个token的例子。因为没有一个统一的系统时钟，所以各个部分的snapshot不是同一时间完成的。我们假设这样一个场景：token在p上的时候（也就是第一幅图），在p上做一个snapshot；然后p发送token到了c（第二幅图）上，此时对c，c’已经q做一个snapshot。把这几个snapshot集合起来，我们发现，p和c上都有token，而这种状态是永远不可能出现的。（即不可能有现有状态转化过来）

再仔细分析一下原因。我们假设p在进行snapshot之前，发送了n个信息；而c在snapshot之前，它的来源发送了n’个信息。上文出现的问题，就是因为n’ > n。
反过来。token在p上，我们对c做一个snapshot；然后等到token发送到了c上，再对p，q，c’做一个snapshot；这时候，我们发现整个snapshot没有任何token，这种状态显然也是不正常的。而不正确的原因是 n’ < n。
我们就可以得到一个结论，为了让snapshot正确（即reachable frome某个真实存在的状态S),必须保证 n == n’。
上面关于channel的讨论，都是来源的process和channel的关系；同理，设q在snapshot之前，接受了m个信息；而c在snapshot之前，向q发送了m’个信息，我们也可以得到结论，m == m’。
又因为 $n^{\prime} \geq m^{\prime}$，$n \geq m$

（好吧，我承认这一段很拗口，我自己看的时候也很费劲。可以对照上面那张图仔细看，下面这一段更拗口）channel记录的数据，必须是发送者record之前发送的数据，减去接受者record之前，收到的数据。只有这样，在c被record的时候，它看到的n’实际上分成两个部分，一个是m’，另外一个是自己记录下来的n’-m’个信息。所以说n’==n。是这么理解的。而m’==m就更好理解，因为c只记录大于m’的信息，就是说我知道这部分信息在channel上传，但是没有被接受。

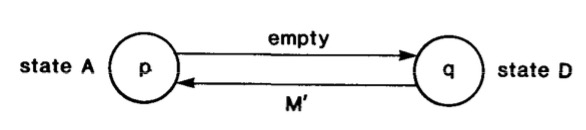
为了方便理解，我画了一张简图。（不要喷图丑，将就着看吧）。这实际上很好的反应了一种状态。p发了n个信息，q收到了m个信息，而n-m个信息正在c上。这时候把阴影部分的信息记录下来，整个snapshot才是合理的。

举个例子，如果n’==m’，那么整个channel一定会是空的，这个很简单；而n’>m’，那么channel必须记录下来(m’+1),(m’+2),…,(n’)个信息。

有了这个概念之后，我们开始想如何设计一个合理的算法，我第一反应是下面的思路：

p在record的时候，立刻不再发信息了，同时记录下来c上的信息（c为空），那么我可以保证n == n’。
然后发送一个marker过去，q收到的时候，做一次record；因为channel上面是FIFO，所以这个marker信息肯定在其他信息到达之后才到达。也就是说，m==n。此时在q上做一个snapshot，可以保证 m == m’。

但是这样是有问题的，为啥呢。因为接受到marker的process，有可能已经record了。那么可能会有这样一个回路，$P_1->P_2->…->P_i->P_1$在$P_1$record的时候，$P_n$肯定也在往channel上发东西。等到$P_n$record的时候，再记录n到1这个channel上为空，但是相对于这个channel，m’肯定大于m了，因为1 record之后到n record之间所有的信息都是m’和m的差值

然而，lamport他们想了另外一个方法:

p在自己record之后，并没有record channel，只是在channel上发送了一个marker。
q在自己record之后，收到了来自某个channel的信息，缓存下来，直到收到来自该channel的marker，然后把这一段时间内缓存的message全都作为c的记录。也就是说，每个channel归自己指向的那个process管理。

我们讨论一下这种算法是否满足前面说的条件。首先关于n和n’，在c被record的时候，说明q已经收到了marker，然后marker之前的所有信息，c上都有，也就是c知道p发了n条信息，n==n’；同理，c没有记录m以内的值，因为c在record的时候，c知道m以内的被q收到了。所以m’==m。

ps: 上面的话我能看懂，但是为啥lamport他们就能相出这种算法我是没明白。从上面四个条件，到这个算法，跳的略微有点大。

3.2 具体算法

其实上面介绍的意见基本差不多了。主要就是两个规则：

Marker-sending Rule: 一个process，一旦record自己的状态之后，对于每个出边的chanel，立刻发送 Marker到channel上。
Marker-receiving Rule: 收到某个Marker的时候，如果没有snapshot：snapshot，同时record该channel为空；
如果已经snapshot，记录channel c为一个message queue，里面包括自己snapshot之后到收到marker之前的信息。

而说明该算法可以有限时间内完成就很简单了，可以理解为BFS?，类似于一个广播，只要能连通的点，肯定能收到marker。而每个节点收到了marker之后会record自己和入边的channel，这样的所有的节点和channel都被record了，一个完整的snapshot就此实现。

3.3 算法的终结

我们可以看到，每个node至多record自己一次；对于每个channel，注定会被它的出边record一次；所以所有的节点和所有的channel最终会被记录一次。而marker是不断传播的，所以算法最终会结束。

4. 算法的正确性

实际上，我们简单地对着这个算法，做一遍token那个例子，从p开始，

p发出一个token，然后发一个marker，record自己；
q收到token，然后发回给p；
q发token给p之后收到marker，record自己，同时把上面的channel记录为空；
p收到了token，缓存下来，然后收到了marker，这时候把token记录到下面的channel上。结束。

如下图所示，可以发现，最终得到的snapshot就是中间的某一个状态。

最终得到的全局snapshot

然而，有时候snapshot并不是其中任意一个状态。但是：这个snapshot可以由开始状态经过某些步骤得到；而由这个snapshot经过有限的步骤，也可以得到最终的状态！

系统的初始状态是一样的。然后从上帝视角来看，由一系列确定有序的event，驱动整个系统：$seq = (e_i, 0 \leq i)$, 假设i个event的时候，我们想要snapshot；第n个event的时候，系统终结。也就是说，snapshot的过程其实就是发生在i到n之间。

然后我们可以找到一个$S^*$，使得:

$S^*$可以从$S_i$ 转化得到；
$S^*$可以转换得到 $S_n$。

实际上我们只需要证明，有另外一个event的序列，和seq所有元素一样，只有在i和n之间调换了顺序；而恰巧$S^*$是中间的一个状态，那么上面两个条件是不是都满足了？严格来说，存在seq’，使得:

对于任意j， j< i, or i >= n: $e_j’ == e_j$
i到n之间的event是seq的一个排列。($e_j, i \leq i < n$)
j < i, or i $\geq$ n, $S_j’ == S_j$
存在k在i和n之间，使得$S^* == S_k’$

Proof
首先定义两个概念：prerecording event和postrecording event，因为event都是在节点上发生的。如果发生在节点做了snapshot，也就是record，之前，称为prerecording，反之postrecording。显然所有小于i的都是prerecording，大于n的都是postrecording。

现在假设这样一种情况，两个相邻的event，前者是postrecording，后者是prerecoding的。如果是在同一个机器上当然是不可能的；但是在不同机器上还是有可能的。（仔细想想是不是）如果我们调换了这二者的顺序，对于结果是不会有影响的。

用反证法，不同节点上的event相互影响只能是发消息，且是前者发消息恰好被后者收到，这种情况下不能调换顺序。假设为$e_j, e_{j+1}$然而，前者是postrecording，所以之前一定有marker在同一个channel上发过了（因为算法的原因，一旦record节点，立刻向所有出边发送marker），根据channel先进先出的原则，这条消息到达之前，marker已经达到了。所以$e_{j+1}$只能是postrecording，矛盾。

所以$e_1,…e_{j-1},e_j,e_{j+1}…$ 和 $e_1,…e_{j-1},e_{j+1},e_j$的效果是一样的。数学归纳法，我们最终可以得到一个序列，使得所有的prerecording的event都在前面。我们设pre和post的event中间的状态是$S^*$

接下来可以证明:

对于每个节点，$ S^* $和真实世界里每个节点record的时候一样（定义，都是执行完所有prerecording event）。也就是说$ S^* $ 中节点的状态和snapshot得到的节点状态是一致的。
对于每个channel，$S^* $记录的状态是（prerecording的event 发送的message）- （prerecording的event 收到的message）。表示这些信息已经被发送了但是没有被接受，正在网络上飞。而之前算法里，记录的是在接受节点record之后，收到marker之前的所有message。这些信息正好就是prerecording 发出的信息，减去prerecording 收到的信息。因为marker之前的信息都是prerecording发出的信息；而prerecording收到的信息，没有被算法记录！所以snapshot算法的channel部分和

至此所有问题全部解决。

5. stability detection

回到之前的论点，对于死锁检测等问题，对于判断函数y，y(S)可以推导出y($S^*$)，所以可以用snapshot的状态来测试S的状态。这就是snapshot的用处。